Berapa banyak sumbu simetri yang dimiliki sebuah lingkaran?
itu sumbu simetri lingkaran Mereka tidak terbatas. Sumbu ini adalah yang membagi bentuk geometris menjadi dua bagian yang persis sama.
Dan lingkaran terdiri dari semua titik yang jaraknya ke titik tetap kurang dari atau sama dengan nilai tertentu "r".
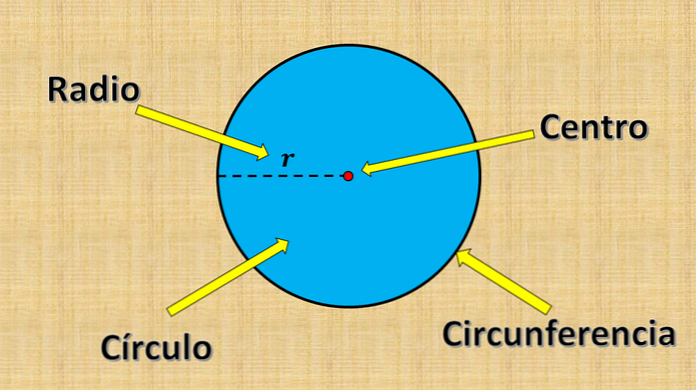
Titik tetap yang disebutkan di atas disebut pusat, dan nilai "r" disebut radius. Jari-jari adalah jarak terbesar yang bisa ada antara titik pada lingkaran dan pusat.
Di sisi lain, setiap segmen garis yang ujungnya berada di tepi lingkaran (keliling) dan melewati pusat disebut diameter. Pengukurannya selalu sama dengan dua kali radius.
Lingkaran dan keliling
Jangan bingung antara lingkaran dengan lingkaran. Lingkar hanya mengacu pada titik-titik yang berjarak "r" dari pusat; yaitu hanya tepi lingkaran.
Namun, ketika mencari sumbu simetri, acuh tak acuh jika Anda bekerja dengan lingkaran atau lingkaran.
Apa itu sumbu simetri?
Sumbu simetri adalah garis yang membagi dalam dua bagian yang sama angka geometris tertentu. Dengan kata lain, sumbu simetri bertindak seperti cermin.
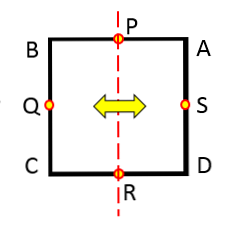
Poros simetri lingkaran
Jika Anda mengamati lingkaran apa pun, terlepas dari jari-jarinya, Anda dapat melihat bahwa tidak setiap garis yang melintasinya adalah sumbu simetri.
Misalnya, tidak ada garis yang digambar dalam gambar berikut adalah sumbu simetri.
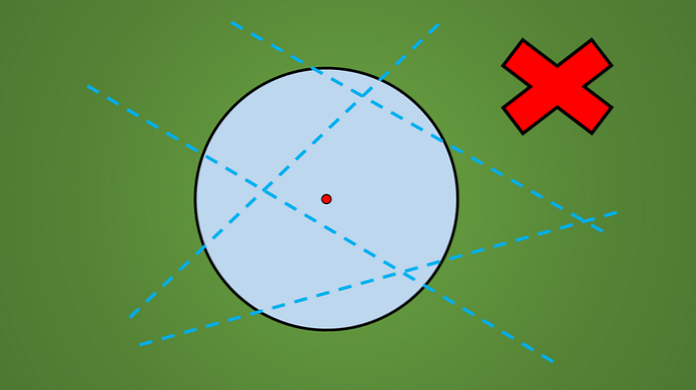
Cara mudah untuk memeriksa apakah suatu garis adalah sumbu simetri atau tidak, adalah dengan memantulkan secara tegak lurus angka geometris ke sisi yang berlawanan dari garis.
Jika refleksi tidak sesuai dengan gambar aslinya, maka garis itu bukan sumbu simetri. Gambar berikut menggambarkan teknik ini.
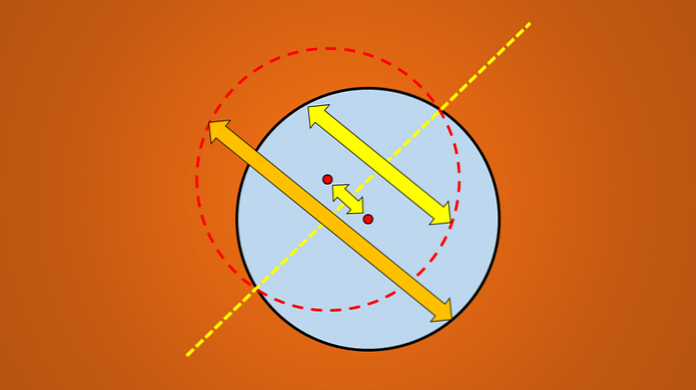
Tetapi jika gambar berikut dipertimbangkan, diketahui bahwa garis yang ditarik adalah sumbu simetri lingkaran.
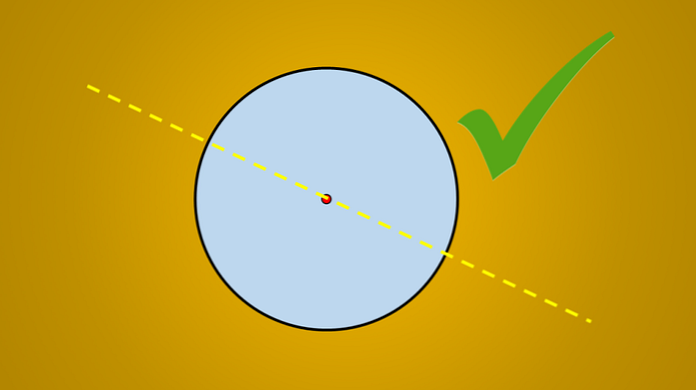
Pertanyaannya adalah: apakah ada lebih banyak sumbu simetri? Jawabannya adalah ya. Jika Anda memutar garis ini 45 ° berlawanan arah jarum jam, garis yang diperoleh juga merupakan sumbu simetri lingkaran.
Hal yang sama terjadi jika Anda memutar 90 °, 30 °, 8 ° dan, secara umum, berapa pun derajatnya.
Yang penting tentang garis-garis ini bukanlah kecenderungan yang mereka miliki, tetapi mereka semua melewati pusat lingkaran. Oleh karena itu, setiap garis yang mengandung diameter lingkaran adalah sumbu simetri.
Jadi, karena sebuah lingkaran memiliki jumlah diameter yang tak terbatas, maka ia memiliki jumlah sumbu simetri yang tak terbatas.
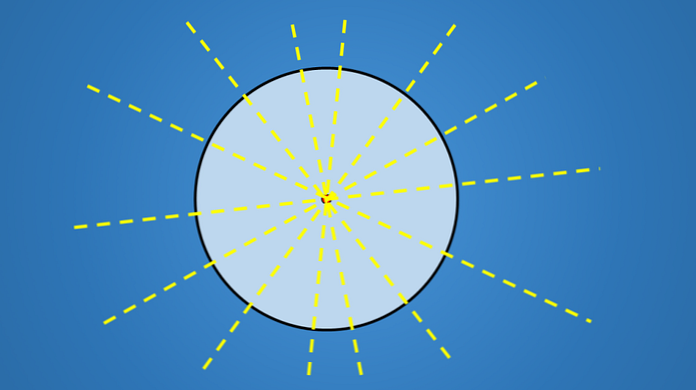
Sosok geometris lainnya, seperti segitiga, segi empat, segi lima, segi enam atau poligon lain, memiliki jumlah sumbu simetri yang terbatas..
Alasan mengapa lingkaran memiliki jumlah sumbu simetri yang tak terbatas adalah karena ia tidak memiliki sisi.
Referensi
- Basto, J. R. (2014). Matematika 3: Geometri analitik dasar. Grup Editorial Patria.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: pendekatan pemecahan masalah bagi guru pendidikan dasar. Editor López Mateos.
- Bult, B., & Hobbs, D. (2001). Leksikon matematika (bergambar ed.). (F. P. Cadena, Trad.) Edisi AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Matematika Geometri Reformasi siklus atas dari E.G.B. Kementerian Pendidikan.
- Schneider, W., & Sappert, D. (1990). Manual menggambar teknis praktis: pengantar dasar-dasar gambar teknis industri. Kembalikan.
- Thomas, G. B., & Weir, M. D. (2006). Perhitungan: beberapa variabel. Pendidikan Pearson.


